Aluno que é aluno de verdade, sempre tenta dar aquela enrolada básica ou até mesmo brincadeirinhas. Então veja essas pérolas inacreditáveis.
Pérola do Limite:
Pérola da Expansão:
Pérola da Raiz:
Pérola do Seno:

Pérola do X:
Na questão acima, vale a pena ressaltar a nota que ele recebeu: - 0,5
Pérola da Conversão:

Pérola do Gráfico:
Pérola da Soma:
y= 1 + 1
y= 3
IGUAL A TRÊS? Como assim?
Por fim, um descanso aos professores na hora de corrigirem as provas.

Atenção: Não faça isso em sua prova!







 ,
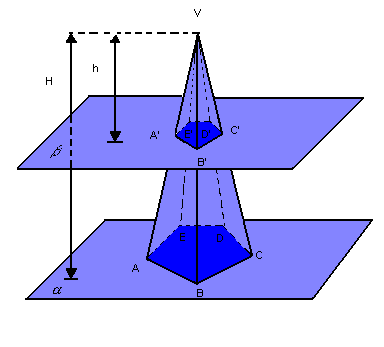
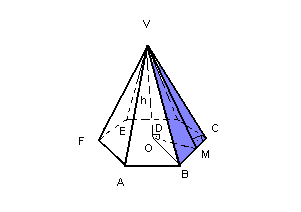
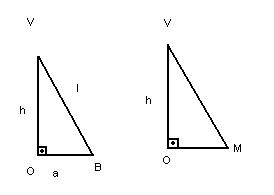
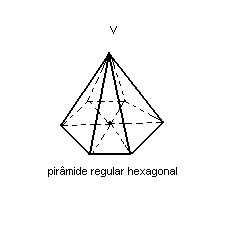
e um ponto V ( vértice) fora de
,
e um ponto V ( vértice) fora de 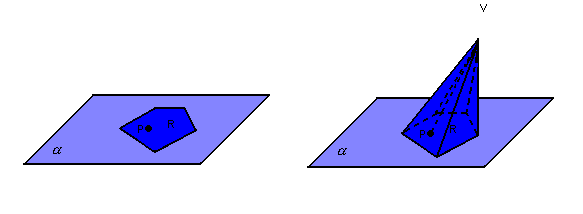
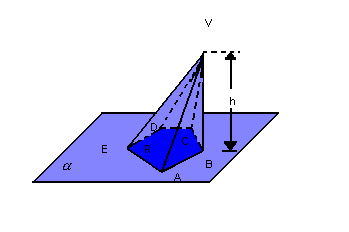
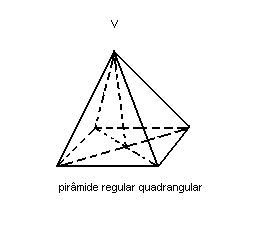













.jpg)
.jpg)
